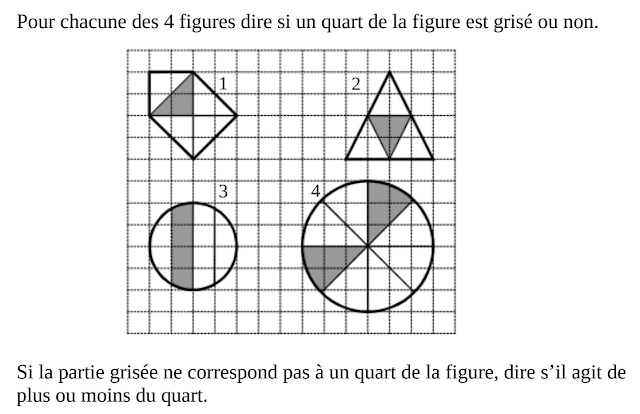
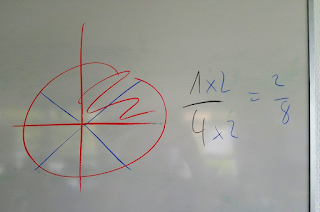La figure 1 ne pose pas de soucis. Tout le monde s'accorde à dire que la figure est partagée en 5 parts égales et pas en 4. Donc la partie grisée correspond à 1/5. Est-ce plus ou moins qu'un quart? Moins car on a partagé en plus de parties donc les parties obtenues sont plus petites.
Pour la figure 2, il y a aussi accord total: la figure est partagée en 4 parts égales donc la partie grisée correspond à 1/4.
La figure 3 amène discussion... Certains pensent que la partie grisée représente 1 quart de la figure car "c'est une partie sur 4". La classe explique (avec du mal) pourquoi le raisonnement est erroné: "les parts ne sont pas toutes pareilles" En effet dans la figure 2, toutes les parties de la figures avaient la même aire... Pas dans la 3. Le partage n'est pas équitable donc la partie grise ne correspond pas à 1/4.. Est-ce plus ou moins? C'est plus car si on prend la part grise 4 fois , cela fait plus que l'unité (car la part grise est plus grande que les parts "sur le côté").
La figure 4 amène aussi une discussion... mais pas sur le fait que c'est 1/4 car tout le monde semble d'accord la dessus. Mais sur pourquoi.
Certains disent: "si je déplace les parties grisées pour les collées, ça ma fait 1/4".
D'autres: "il y a 2 parts grises sur 8 et 2 c'est la quart de 8".
Ou encore : "si on compte les parts 2 par 2, ça fait 4 groupes, et un seul est grisé".
Pour finir: "2 sur 8 c'est comme 1 sur 4 car 1 c'est la moitié de 2 et 4 la moitié de 8".
Cela permet de montrer à la classe:
En partageant chaque quart en 2, j'obtiens deux fois plus de parts (2x4 = 8) mais elles sont deux fois plus petites et j'en "prends" deux fois plus. Donc 1/4 = 2/8.
Autrement dit, si je partage 2 fois plus mais que je prends 2 fois plus de parts, cela ne change pas ma fraction.