Frise

 

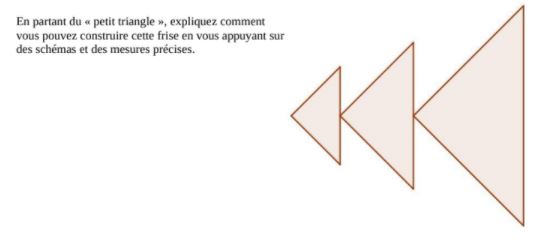
Les élèves comprennent bien l'enjeu et ne se limitent pas à décrire la figure (un petit triangle puis un moyen...). Ils se lancent tous dans la prises de mesures et la recherche d'un agrandissement.

Très bien... Sauf qu'un agrandissement n'est pas un déplacement. Quand on agrandit une figure, on multiplie les longueurs de ses côtés par la même valeur mais il n'y a pas "d'histoire de positionnement".

Quelques élèves ont remarqué qu'il faut faire une translation avant d'agrandir. Mais agrandir n'est toujours pas un déplacement.

J’explique alors qu'on peut faire un agrandissement par rapport à un point.
Par exemple, si on fait une translation du petit triangle de tel sorte qu'il se superpose avec "le moyen".
Une fois déplacé ainsi, on peut l'agrandir par rapport au sommet commun. C'est à dire qu'en plus de l'agrandir, on va "repousser" les points.

Cette transformation s'appelle une homothétie: elle a un centre (le point "à partir duquel on agrandit) et un coefficient (combien de fois on agrandit).

On peut aussi faire une autre transformation qui permet de ne pas faire de translation:

Je leur propose de relier les sommets des triangles entre eux:

On remarque que les droites ainsi obtenues se croisent en un point (qu'on appelle O).

On regarde alors la distance des triangles par rapport à ce point O et on remarque que le triangle 2, en plus d'être, en terme de longueur, 1,5 fois plus grand que le triangle 1, il est aussi 1,5 fois plus loin que le triangle 1 du point O.

On a ce qu'on appelle une homothétie de centre O et de coefficient 1,5.

Cette notion n'est pas facile à appréhender. On fait d'autres exemples et on le reverra plus tard.