Tarifs location de voiture

 

 

 

Certains font des essais (de manière plus ou moins organisée...)
 

D'autres utilisent un autre raisonnement (plus efficace): avec le tarif B on gagne 4 € par km (9-5=4) mais on donne 30€ au début. Donc, il faut 30:4 = 7,5 km pour récupérer les 30€.

Enfin un élève, propose de représenter par x le nombre de km parcourus. 

Avec le tarif A, on paiera 9 x x € et avec le tarif B, on paiera: 30 + 5 x x €.

Pour chercher quand les 2 tarifs sont au même prix il faut résoudre l'équation:  

9 x x =30 + 5 x x

 

Après avoir expliqué cela, on regarde comment représenter les essais effectués. Je propose de remplir :

 

 

 

Voici ce que cela donne:

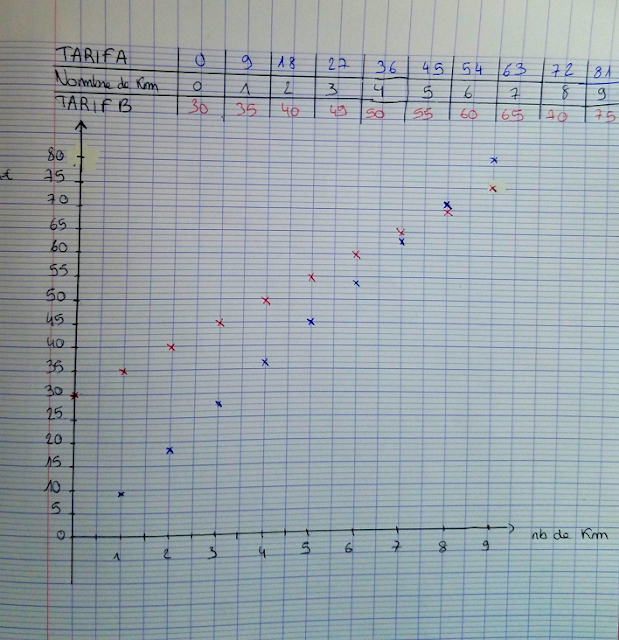
On analyse de plus près les 2 tarifs.
On utilise pour commencer le tableau. Beaucoup d'élèves, ont rempli la ligne du bas en rajoutant 5 à chaque fois. 

Autrement dit,  pour chaque km parcouru le prix augmente de 5€.
De même pour le tarif A, pour chaque km parcouru le prix augmente de 9€.

Dans les 2 cas, le prix augmente régulièrement en fonction des km parcourus. On peut dire que les 2 situations sont des situations affines.

On remarque également que pour le tarif A, "c'est la table du 9". On multiplie par 9 le nombre de km pour déterminer le prix. Autrement dit, le prix en € est 9 fois plus grand que le nombre de km. C'est une situation de proportionnalité.
Est-ce le cas pour le tarif B? " non à cause des 30€".

Donc les deux tarifs donnent lieu à une augmentation régulière en fonction des km, on parle de situations affine. Mais seul le tarif A est proportionnel au nombre de km.

 On fait maintenant l'analyse du graphique (en sachant déjà ce qu'on veut voir):

 - pour les 2 tarifs les points sont alignés. Pourquoi? Car les 2 tarifs augmentent régulièrement (situations affines).
- le tarif A "passe par 0". Donc il est proportionnel au nombre de k. Pas le tarif B qui "part de 30".

Donc les situations qui varient régulièrement (affines) sont représentées par des points alignés et quand en plus d'être régulière la situation est proportionnelle, les points sont alignés avec l'origine du repère (le 0).